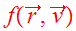 which implies a time-independent
which implies a time-independent
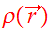 .
Introducing the notation
.
Introducing the notation
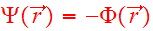 and
and
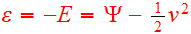 ,
a very simple form for the distribution function
,
a very simple form for the distribution function
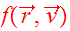 is
is
Consider a steady state star cluster with time-independent
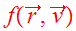 which implies a time-independent
which implies a time-independent
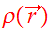 .
Introducing the notation
.
Introducing the notation
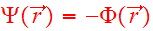 and
and
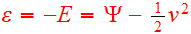 ,
a very simple form for the distribution function
,
a very simple form for the distribution function
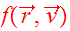 is
is
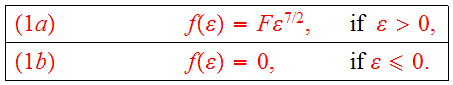
Eq.(1a,1b) defines Plummer's model. Calculate the density function
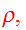
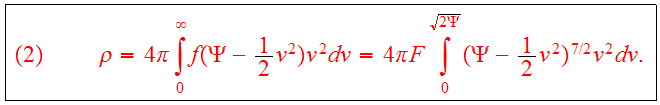
If we make the substitution
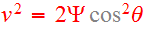 ,
,
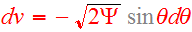 ,
this becomes
,
this becomes
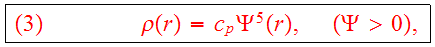
where


In Plummer's model the density rises as the
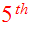 power of
power of
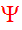 when
when
 ,
and is, of course, zero when
,
and is, of course, zero when
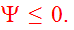 When we use Eq.(3) to eliminate
When we use Eq.(3) to eliminate
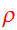 from Poisson's equation, we find
from Poisson's equation, we find
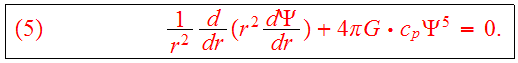
If we eliminate
 and
and
 from Eq.(5) in favor of the rescaled variables,
from Eq.(5) in favor of the rescaled variables,
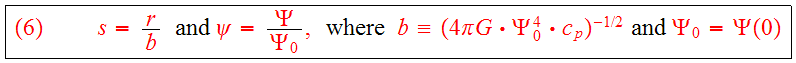
then Eq.(5) takes the simple form
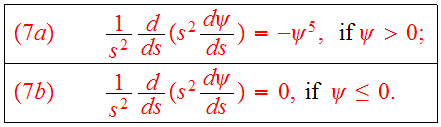
The solution of Eqs.(7a,7b) is given by
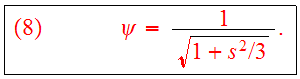
The corresponding density is
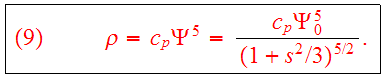
Note that the density is everywhere non-zero. The total mass is finite, however, with the value
